최소제곱법 (Ordinary Least Squares) 과 선형회귀 알고리즘 (Linear Regression)

이번 포스팅에서는 최소제곱법(Least Ordinary Sqaures)의 Python 코드 구현과 scikit-learn의 LinearRegression을 활용하여 회귀(Regression) 예측까지 해보겠습니다.

코드

Colab으로 열기

GitHub에서 소스보기

최소제곱법 (Ordinary Least Squares)?

최소제곱법, 또는 최소자승법, 최소제곱근사법, 최소자승근사법(method of least squares, least squares approximation)은 어떤 계의 해방정식을 근사적으로 구하는 방법으로, 근사적으로 구하려는 해와 실제 해의 오차의 제곱의 합이 최소가 되는 해를 구하는 방법입니다.

한계

• 노이즈(outlier)에 취약합니다.
• 특징 변수와 샘플 건수에 비례해서 계산 비용이 높습니다.

RSS(Residual Sum of Square) 공식

실제 값(y)과 가설(y_hat)에 의한 예측 값의 차이가 가장 작은 계수 계산

선형함수:

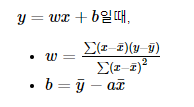
샘플 데이터를 생성합니다.

import numpy as np
import matplotlib.pyplot as plt

# 50개의 X를 생성합니다.
x = np.arange(50)

# a=기울기, b=절편
a = 0.3
b = 0.8

# 선형회귀 식을 작성합니다. y 값을 산출합니다.
y = a * x + b

위의 수식에 근거하여 y 데이터 생성시 일직선으로 표현되는 단순한 선형함수가 완성되므로, 약간의 노이즈를 추가합니다.

# 노이즈를 랜덤하게 생성합니다.
noise = np.random.uniform(-1.25, 1.25, size=y.shape)

# y 값에 노이즈를 추가합니다.
yy = y + noise

plt.figure(figsize=(10, 7))
plt.plot(x, y, color='r', label='y = 0.3*x + b')
plt.scatter(x, yy, label='data')
plt.legend(fontsize=18)
plt.show()

샘플 데이터 생성 코드를 함수로 만들기

def make_linear(w=0.5, b=0.8, size=50, noise=1.0):
    x = np.arange(size)
    y = w * x + b
    noise = np.random.uniform(-abs(noise), abs(noise), size=y.shape)
    yy = y + noise
    plt.figure(figsize=(10, 7))
    plt.plot(x, y, color='r', label=f'y = {w}*x + {b}')
    plt.scatter(x, yy, label='data')
    plt.legend(fontsize=20)
    plt.show()
    print(f'w: {w}, b: {b}')
    return x, yy

x, y = make_linear(size=50, w=1.5, b=0.8, noise=5.5)

w: 1.5, b: 0.8

Python 코드로 구현

최소제곱법 (Least Square) 공식

RSS(Residual Sum of Square)

실제 값(y)과 가설(y_hat)에 의한 예측 값의 차이가 가장 작은 계수 계산

선형함수:

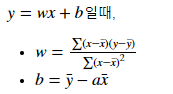
x_bar(x 평균), y_bar (y 평균) 구하기

x_bar = x.mean()
y_bar = y.mean()

w의 계수 값 찾기

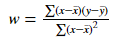
calculated_weight = ((x - x_bar) * (y - y_bar)).sum() / ((x - x_bar)**2).sum()
print('w: {:.2f}'.format(calculated_weight))

w: 1.51

b의 계수 값 구현

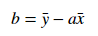
calculated_bias = y_bar - calculated_weight * x_bar

print('b: {:.2f}'.format(calculated_bias))

b: 0.01

노이즈 값을 증가 시켰을 때

최소제곱법은 노이즈에 취약하다는 단점이 있습니다.

이를 직접 눈으로 확인해 보도록 하겠습니다.

x, y = make_linear(size=100, w=0.7, b=0.2, noise=5.5)
# 임의로 2개의 outlier를 추가해 보도록 하겠습니다.
y[5]=60
y[10]=60
plt.figure(figsize=(10, 7))
plt.scatter(x, y)
plt.show()

w: 0.7, b: 0.2

# 위에서 구한 w, b 찾는 공식을 그대로 적용합니다.
x_bar = x.mean()
y_bar = y.mean()
calculated_weight = ((x - x_bar) * (y - y_bar)).sum() / ((x - x_bar)**2).sum()
calculated_bias = y_bar - calculated_weight * x_bar

print('w: {:.2f}, b: {:.2f}'.format(calculated_weight, calculated_bias))

w: 0.63, b: 4.26

위의 결과에서도 볼 수 있듯이, outlier에 취약합니다.

근본적으로 x, y의 평균 값을 활용하여 기울기 (w)와 절편 (b)를 구하게 될 때, outlier가 크게 영향을 끼치는 것을 볼 수 있습니다.

최소제곱법 (OLS)를 활용한 LinearRegression

scikit-learn 패키지의 LinearRegression이 바로 최소 제곱 추정 방식으로 회귀 예측 알고리즘 입니다.

LinearRegression 도큐먼트

from sklearn.linear_model import LinearRegression

model = LinearRegression()

model.fit(x.reshape(-1, 1), y)

LinearRegression(copy_X=True, fit_intercept=True, n_jobs=None, normalize=False)

print('w: {:.2f}, b: {:.2f}'.format(model.coef_[0], model.intercept_))

w: 0.63, b: 4.26