🔥알림🔥
① 테디노트 유튜브 -
구경하러 가기!
② LangChain 한국어 튜토리얼
바로가기 👀
③ 랭체인 노트 무료 전자책(wikidocs)
바로가기 🙌
④ RAG 비법노트 LangChain 강의오픈
바로가기 🙌
⑤ 서울대 PyTorch 딥러닝 강의
바로가기 🙌
의사결정 나무 (Decision Tree)와 Entropy, 그리고 Gini 계수
Decision Tree는 Random Forest Ensemble 알고리즘의 기본이 되는 알고리즘이며, Tree 기반 알고리즘입니다. 의사결정나무 혹은 결정트리로 불리우는 이 알고리즘은 머신러닝의 학습 결과에 대하여 시각화를 통한 직관적인 이해가 가능하다는 것이 큰 장점입니다. 더불어, Random Forest Ensemble 알고리즘은 바로 이 Decision Tree 알고리즘의 앙상블 (Ensemble) 알고리즘인데, Random Forest 앙상블 알고리즘이 사용성은 쉬우면서 성능까지 뛰어나 캐글 (Kaggle.com)과 같은 데이터 분석 대회에서 Baseline 알고리즘으로 많이 활용되고 있습니다.
이번 실습에서는 Decision Tree 알고리즘에 대하여 시각화, Entropy와 Gini 계수에 대한 상세한 이해를 돕고자 만들어진 튜토리얼 이며, 실습 후반부에는 자주 사용되는 Hyperparameter 에 대한 소개도 진행합니다.
Random Forest 의 Hyperparameter와 겹치는 부분이 많기 때문에, 본 실습을 통해 Hyperparameter에 대하여 숙지해 두시면 자동으로 Random Forest 알고리즘의 Hyperparameter에 대한 이해까지 할 수 있게되는 1석 2조의 효과를 보실 수 있습니다.
코드
from IPython.display import Image
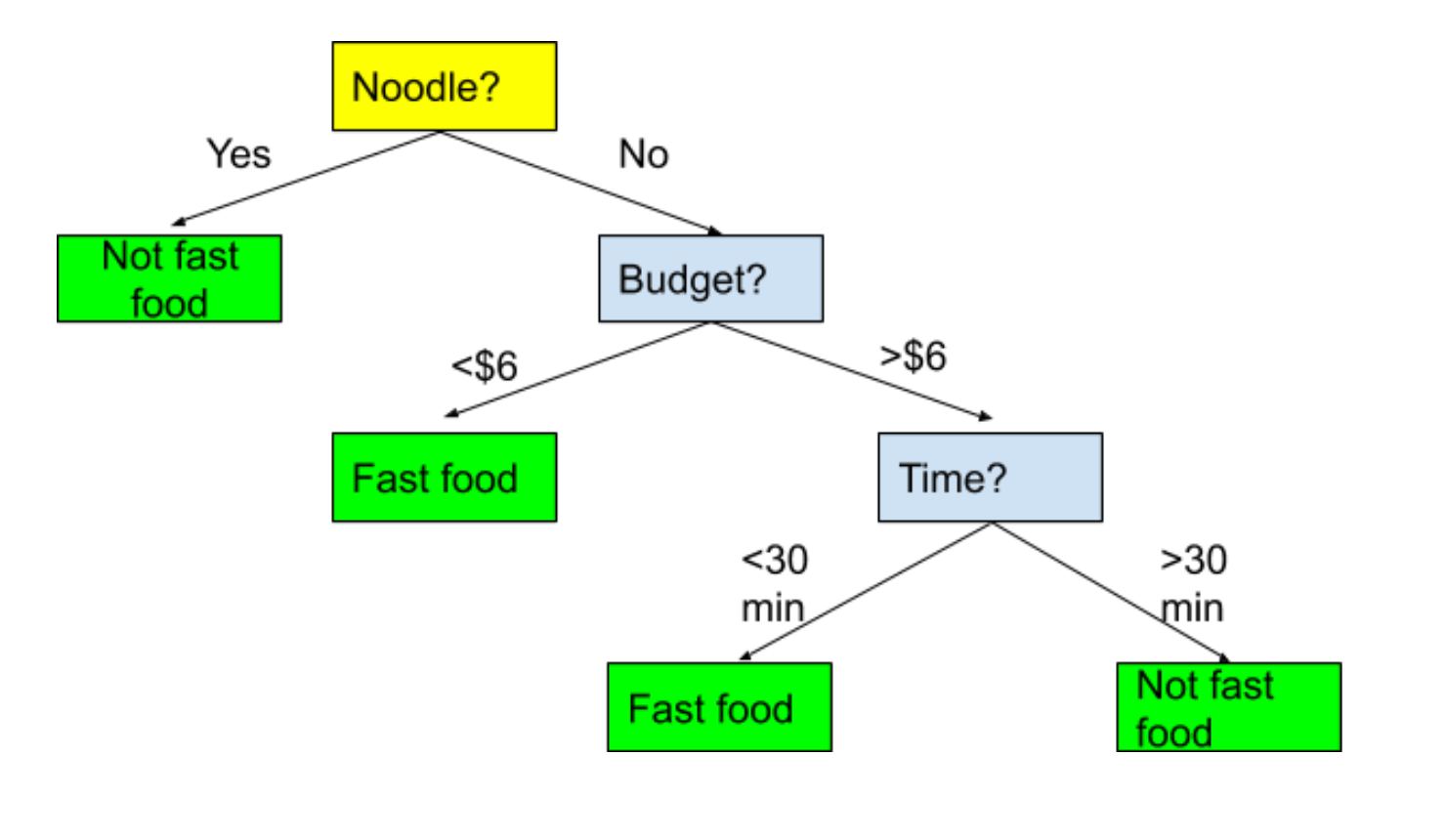
결정트리 or 의사결정나무 (Decision Tree)
결정트리를 가장 단수하게 표현하자면, Tree 구조를 가진 알고리즘입니다.
의사결정나무는 데이터를 분석하여 데이터 사이에서 패턴을 예측 가능한 규칙들의 조합으로 나타내며, 이 과정을 시각화 해 본다면 마치 스무고개 놀이와 비슷합니다.
Image(url='https://miro.medium.com/max/2960/1*dc_342kIsHCzuko1TtyEGQ.png', width=500)
결정트리의 기본 아이디어는 sample이 가장 섞이지 않은 상태로 완전히 분류되는 것, 다시 말해서 엔트로피(Entropy)를 낮추도록 만드는 것입니다.
엔트로피 (Entropy)
엔트로피는 쉽게 말해서 무질서한 정도를 정량화(수치화)한 값입니다.
다음은 엔트로피 지수를 방이 어질러있는 정도를 예시로 들어 표현되었습니다.
Image(url='https://image.slidesharecdn.com/entropyandthe2ndlaw-120327062903-phpapp02/95/103-entropy-and-the-2nd-law-3-728.jpg?cb=1335190079', width=500)
엔트로피 수식의 이해
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 샘플데이터를 생성합니다.
group_1 = np.array([0.3, 0.4, 0.3])
group_2 = np.array([0.7, 0.2, 0.1])
group_3 = np.array([0.01, 0.01, 0.98])
fig, axes = plt.subplots(1, 3)
fig.set_size_inches(12, 4)
axes[0].bar(np.arange(3), group_1, color='blue')
axes[0].set_title('Group 1')
axes[1].bar(np.arange(3), group_2, color='red')
axes[1].set_title('Group 2')
axes[2].bar(np.arange(3), group_3, color='green')
axes[2].set_title('Group 3')
plt.show()
Image(url='https://miro.medium.com/max/1122/0*DkWdyGidNSfdT1Nu.png', width=350)
# entropy를 구현합니다.
def entropy(x):
return (-x*np.log2(x)).sum()
Entropy 계산 및 시각화
entropy_1 = entropy(group_1)
entropy_2 = entropy(group_2)
entropy_3 = entropy(group_3)
print(f'Group 1: {entropy_1:.3f}\nGroup 2: {entropy_2:.3f}\nGroup 3: {entropy_3:.3f}')
plt.figure(figsize=(5, 5))
plt.bar(['Group 1', 'Group 2', 'Group 3'], [entropy_1, entropy_2, entropy_3])
plt.title('Entropy', fontsize=15)
plt.show()
지니 계수 (Gini Index)
- 클래쓰들이 공평하게 섞여 있을 수록 지니 계수는 올라갑니다.
- Decision Tree는 지니 불순도를 낮추는 방향으로 가지치기를 진행합니다.
Image(url='http://www.learnbymarketing.com/wp-content/uploads/2016/02/gini-index-formula.png', width=350)
# Gini Index 구현합니다.
def gini(x):
return 1 - ((x / x.sum())**2).sum()
# 샘플데이터를 생성합니다.
group_1 = np.array([50, 50])
group_2 = np.array([30, 70])
group_3 = np.array([0, 100])
fig, axes = plt.subplots(1, 3)
fig.set_size_inches(12, 4)
axes[0].bar(['Positive', 'Negative'], group_1, color='blue')
axes[0].set_title('Group 1')
axes[1].bar(['Positive', 'Negative'], group_2, color='red')
axes[1].set_title('Group 2')
axes[2].bar(['Positive', 'Negative'], group_3, color='green')
axes[2].set_title('Group 3')
plt.show()
gini_1 = gini(group_1)
gini_2 = gini(group_2)
gini_3 = gini(group_3)
print(f'Group 1: {gini_1:.3f}\nGroup 2: {gini_2:.3f}\nGroup 3: {gini_3:.3f}')
plt.figure(figsize=(5, 5))
plt.bar(['Group 1', 'Group 2', 'Group 3'], [gini_1, gini_2, gini_3])
plt.title('Gini Index', fontsize=15)
plt.show()
Decision Tree 구현
from sklearn.tree import DecisionTreeClassifier
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
SEED = 42
# breast cancer 데이터셋 로드
cancer = load_breast_cancer()
# train, test 데이터 분할
x_train, x_test, y_train, y_test = train_test_split(cancer['data'], cancer['target'], stratify=cancer['target'], random_state=SEED)
# 알고리즘 정의
tree = DecisionTreeClassifier(random_state=0)
# 학습
tree.fit(x_train, y_train)
# 예측
pred = tree.predict(x_test)
# 정확도 측정
accuracy = accuracy_score(pred, y_test)
print(f'Accuracy Score: {accuracy:.3f}')
의사결정나무 시각화
from sklearn.tree import export_graphviz
from sklearn.metrics import accuracy_score
import graphviz
def show_trees(tree):
export_graphviz(tree, out_file="tree.dot", class_names=["악성", "양성"],
feature_names=cancer['feature_names'],
precision=3, filled=True)
with open("tree.dot") as f:
dot_graph = f.read()
pred = tree.predict(x_test)
print('정확도: {:.2f} %'.format(accuracy_score(y_test, pred) * 100))
display(graphviz.Source(dot_graph))
show_trees(tree)
주요 Hyper Parameter
max_depth
max_depth는 최대 트리의 깊이를 제한 합니다.
기본 값은 None, 제한 없음 입니다.
tree = DecisionTreeClassifier(max_depth=3, random_state=SEED)
tree.fit(x_train, y_train)
show_trees(tree)
min_sample_split
min_sample_split은 노드 내에서 분할이 필요한 최소의 샘플 숫자입니다.
기본 값은 2입니다.
tree = DecisionTreeClassifier(max_depth=6, min_samples_split=20, random_state=SEED)
tree.fit(x_train, y_train)
show_trees(tree)
min_samples_leaf
min_samples_leaf는 말단 노드의 최소 샘플의 숫자를 지정합니다.
기본 값은 1 입니다.
DecisionTreeClassifier()
max_leaf_nodes
max_leaf_nodes는 말단 노드의 최대 갯수 (과대 적합 방지용)
기본 값은 None, 제한 없음 입니다.
tree = DecisionTreeClassifier(max_depth=7, max_leaf_nodes=10, random_state=SEED)
tree.fit(x_train, y_train)
show_trees(tree)
max_features
최적의 분할을 찾기 위해 고려할 피처의 수
0.8 은 80% 의 feature 만 고려하여 분할 알고리즘 적용
기본 값은 None, 모두 사용입니다.
tree = DecisionTreeClassifier(max_depth=7, max_features=0.8, random_state=SEED)
tree.fit(x_train, y_train)
show_trees(tree)
feature의 중요도 파악
feature_importances_ 변수를 통해서 tree 알고리즘이 학습시 고려한 feature 별 중요도를 확인할 수 있습니다.
tree.feature_importances_
DataFrame으로 만들면 중요도(feature importances) 순서로 정렬할 수 있습니다.
df = pd.DataFrame(list(zip(cancer['feature_names'], tree.feature_importances_)), columns=['feature', 'importance']).sort_values('importance', ascending=False)
df = df.reset_index(drop=True)
df.head(15)
plt.figure(figsize=(10, 10))
sns.barplot(y='feature', x='importance', data=df)
plt.show()





댓글남기기